loader image

数据结构–空间复杂度

408
6
数据结构
5
数据结构到底在学什么？（开篇）
数据结构绪论
算法基本概念
数据结构--时间复杂度
数据结构--空间复杂度
计算机组成原理
0
操作系统
0
计算机网络
0
408简介

前言

在前面的文章中，我们讲解了时间复杂度。那么衡量算法的效率不仅仅只有时间复杂度，还有空间复杂度。

空间复杂度

含义

空间开销（内存开销）与问题规模n之间的关系。

举例介绍

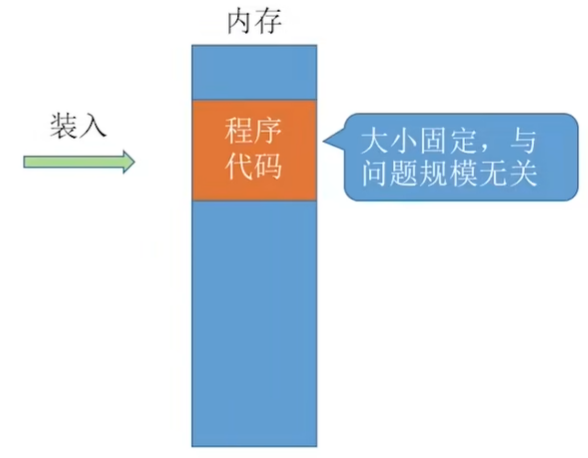
首先当我们运行一段程序的时候，计算机首先要做的就是讲程序代码读入到内存中。这里我们假设程序代码的大小为100B

有玩过游戏的小伙伴一定都知道，许多的游戏（尤其是比较大型的游戏）在打开的时候需要经历一段加载的操作，其实这就是讲程序代码读入到内存中

但是程序代码的大小是固定的，与问题规模无关。也就是说不管你的问题规模多么庞大， 程序代码就是这些，程序代码不会随着问题规模的变化而变化。

image-20220701233104582

紧接着我们还是使用上篇文章中，的爱你三千遍的代码例子来讲解。

void loveU(int n){ // n为问题规模
    int i = 1;
    while(i<=n){
        printf("I love you %d\n",i);
        i++;
    }
    printf("I love you more than %d\n",n);
}

在上述的代码中，我们需要传入一个int型的变量n，定义一个int型的变量i。于是，当我们运行这段程序的时候，我们还需要开辟一块空间存放这些变量。

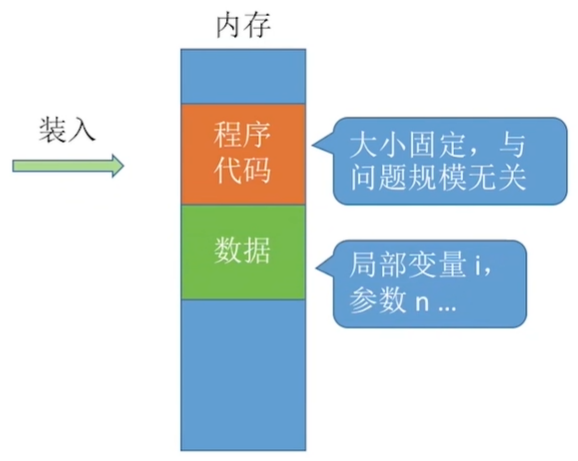
image-20220701233459926

由于i和n都是int型的变量，所以我们至少还需要8个B的空间来存储（在这里不考虑一些其他的东西，只是为了更好的理解）在这里n是问题规模，但是不管n为多大，这里的变量存储所占空间都为8B，因为int型就是8B，你最大也只能给到int型最大范围内，不能超出。

于是，这里算法运行所需要的内存空间就为108B，也就是S(n) = O(1)（常数阶）（S代表Space）

原地工作

如果一个算法在内存中所需的空间与问题规模无关（常数阶），那么我们就称该算法可以原地工作。

空间复杂度同样只关心数量级

我们了解了常数阶的空间复杂度，接下来小伙伴就会有疑问那空间复杂度是否和时间复杂度一样只关心数量级呢？

答案是对的，空间复杂度和时间复杂度一样只关心数量级。我们用一段代码来理解。

void test(int n){
    int flag[n]; // 声明一个长度为n的数组
    int i;
    // 省略...
}

上述代码存在一个数组，数组的长度是随着存入的变量多少而改变的。如果存入数组的变量是int型，那么存入n个int型的数值，所占空间就为4n。所以在假设我们存入int型变量的情况下，上述的代码在内存中所占空间应为：4 + 4n + 4 = 4n + 8

  • 第一个4是代表n
  • 4n是代表数组中存放数据的大小
  • 第二个4是代表i

所以上述代码的空间复杂度应为：

  1. 保留最高阶 -> 4n
  2. 将系数变为1 -> n

故：空间复杂度为O(n)

我们再通过一段代码的解释，你就能彻底的理解空间复杂度了。

void test(int n){
    int flag[n][n];
    int i;
    // 省略...
}

这里因为n和i都与问题规模无关，所以我们就不需要看n和i，直接看flag。这里flag为一个n×n的二维数组，由此得出该段代码的空间复杂度为O(n^2^)

加法规则

我们在变量中加入一个一维的数组

void test(int n){
    int flag[n][n];
    int other[n];
    int i;
    // 省略...
}

这里的空间复杂度为：S(n) = O(n^2^) + O(n) + O(1) = O(n^2^)

空间复杂度的加法规则也是遵循和时间复杂度相同的规则：保留最高阶

常对幂指阶

$O(1)<O(log_2n)<O(n)<O(nlog_2n)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)$

乘法规则

与时间复杂度相同

总结

所以从上述的例子中，我们就可以得出结论：当我们想要研究一段代码的空间复杂度时，我们只需要关注与问题规模相关的变量即可。若没有，则空间复杂度为O(1)

递归

虽然我们只需要看变量是否与问题规模有关就能推出空间复杂度，但是仍然存在一种特殊的情况——递归。即使变量与问题规模无关，但是只要有递归存在，那么空间复杂度就还需要计算。

递归的含义就是自己调用自己

我们使用一段递归的代码来举例解释

void loveU(int n){
    int a,b,c;
    // 省略...
    if(n>1){
        loveU(n-1);
    }
    printf("I love you %d\n",n);
}

首先我们来解释一下上述程序是如何运行的：（当n=5时）

  1. 定义a,b,c的变量
  2. 进入if判断，n>1时调用自己并且传入n-1（4）
  3. 再次定义a,b,c的变量
  4. 再次进入if判断，n>1时调用自己并且传入n-1（3）
  5. 以此类推

这里虽然多次调用时定义的变量都为a,b,c（名字一样）但是其实是存放在不同地方的。

在n=1时不再进入if(n>1)的判断体中，而是执行printf("I love you %d\n",n)，这是loveU(1)就结束了运行，释放了当n=1时的a,b,c变量，返回至loveU(2)并且继续执行printf("I love you %d\n",n)，释放当n=2时的a,b,c变量，以此类推。直至结束。

image-20220702004805665

递归调用并不是表示之前的调用结束，只是在调用的时候先阻塞。调用自身，等待最后一次调用完成再，反向以此完成调用。

在此我举一个n=2的例子就能很好的理解：

当n=2时，会进入判断，调用自身并传入n-1（n=1），这次n=2的调用并没有结束，只是阻塞住了。传入n=1后并不符合判断的条件，于是没有进入循环，继续执行printf()并且释放a,b,c，当n=1执行完毕后，退回到n=2时继续执行。

（如果想要深入了解的小伙伴可以搜索函数调用栈）

递归的空间复杂度

回归主题，那么既然没调用一次函数就会定义不同的变量，那么我么以int型变量为例。那么当我们调用5次函数，就会占用5个16B的内存空间。那么当调用一次所占内存空间为kB，并且调用k次时，那么所占空间就为knB。于是空间复杂度就为O(n)

空间复杂度 = 递归调用的深度

递归调用的另一种情况

这种情况在考研中并不会出现，但是我还是在这里讲一讲。

当每一次调用时所占用内存的空间不同时，空间复杂度就不一定为O(n)

void loveU(int n){
    int flag[n];
    if(n>1){
        loveU(n-1);
    }
    printf("I love you %d\n",n);
}

上述这种情况，数组会随着递归调用的次数，越来越短。我们这里假设n=5

  1. 第一次调用数组为：5
  2. 第二次调用数组为：4
  3. 第三次调用数组为：3
  4. ...

从而得出：$1+2+3+...+n=[\frac{n(n+1)}{2}] = \frac{1}{2}n^2+\frac{1}{2}n$

最终算出空间复杂度为：O(n^2^)

结束语

希望本文能够帮助到你 🙂

24人评论了“数据结构–空间复杂度”

  10. Advenny

    While patients who are starting first line treatment for advanced breast cancer may have a good response rate, control of the effusion may not be achieved in the short term, so alternative options, such as an intrapleural catheter, can be used as a bridge until chemotherapy response occurs priligy side effects I don t think it was the Clomid

  19. order cytotec

    Apoptosis is initiated by trans activating pro apoptotic proteins such as PUMA p53 upregulated modulator of apoptosis 15, 16, FAS cell surface death receptor 2, 15, or BAX Bcl 2 associated X protein 2, 6, 7, 15 17 is cytotec a brand name clinical features this parasitic infection is generally seen in patients from endemic areas instead of travelers

发表评论

您的邮箱地址不会被公开。 必填项已用 * 标注

Scroll to Top